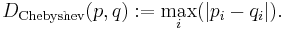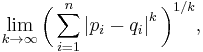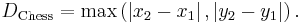Chebyshev distance

a b c d e f g h
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
a b c d e f g h
The Chebyshev distance between two spaces on a chess board gives the minimum number of moves a king requires to move between them. This is because a king can move diagonally, so that the jumps to cover the smaller distance parallel to a rank or column is effectively absorbed into the jumps covering the larger. Above are the Chebyshev distances of each square from the square f6.

In mathematics, Chebyshev distance (or Tchebychev distance), Maximum metric, or L∞ metric[1] is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension.[2] It is named after Pafnuty Chebyshev.

It is also known as chessboard distance, since in the game of chess the minimum number of moves needed by a king to go from one square on a chessboard to another equals the Chebyshev distance between the centers of the squares, if the squares have side length one, as represented in 2-D spatial coordinates with axes aligned to the edges of the board.[3] For example, the Chebyshev distance between F6 and E2 equals 4.

Contents

Definition

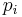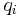The Chebyshev distance between two vectors or points p and q, with standard coordinates p_i and q_i, respectively, is

D_{\rm Chebyshev}(p,q)�:= \max_i(|p_i - q_i|).\

This equals the limit of the Lp metrics:

\lim_{k \to \infty} \bigg( \sum_{i=1}^n \left| p_i - q_i \right|^k \bigg)^{1/k},

hence it is also known as the L∞ metric.

Mathematically, the Chebyshev distance is a metric induced by the supremum norm or uniform norm. It is an example of an injective metric.

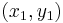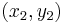In two dimensions, i.e. plane geometry, if the points p and q have Cartesian coordinates (x_1,y_1) and (x_2,y_2), their Chebyshev distance is

D_{\rm Chess} = \max \left ( \left | x_2 - x_1 \right | , \left | y_2 - y_1 \right | \right ) .

Under this metric, a circle of radius r, which is the set of points with Chebyshev distance r from a center point, is a square whose sides have the length 2r and are parallel to the coordinate axes.

On a chess board, where one is using a discrete Chebyshev distance, rather than a continuous one, the circle of radius r is a square of side lengths 2r, measuring from the centers of squares, and thus each side contains 2r+1 squares; for example, the circle of radius 1 on a chess board is a 3×3 square.

Properties

In one dimension, all Lp metrics are equal – they are just the absolute value of the difference.

The two dimensional Manhattan distance also has circles in the form of squares, with sides of length √2r, oriented at an angle of π/4 (45°) to the coordinate axes, so the planar Chebyshev distance can be viewed as equivalent by rotation and scaling to the planar Manhattan distance.

However, this equivalence between L1 and L∞ metrics does not generalize to higher dimensions. A sphere formed using the Chebyshev distance as a metric is a cube with each face perpendicular to one of the coordinate axes, but a sphere formed using Manhattan distance is an octahedron: these are dual polyhedra, but among cubes, only the square (and 1-dimensional line segment) are self-dual polyhedra.

The Chebyshev distance is sometimes used in warehouse logistics.[4]

On a grid (such as a chessboard), the points at a Chebyshev distance of 1 of a point are the Moore neighborhood of that point.

See also

References

  1. ^ Cyrus. D. Cantrell (2000). Modern Mathematical Methods for Physicists and Engineers. Cambridge University Press. ISBN 0521598273. 
  2. ^ James M. Abello, Panos M. Pardalos, and Mauricio G. C. Resende (editors) (2002). Handbook of Massive Data Sets. Springer. ISBN 1402004893. 
  3. ^ David M. J. Tax, Robert Duin, and Dick De Ridder (2004). Classification, Parameter Estimation and State Estimation: An Engineering Approach Using MATLAB. John Wiley and Sons. ISBN 0470090138. 
  4. ^ André Langevin and Diane Riopel (2005). Logistics Systems. Springer. ISBN 0387249710. http://books.google.com/books?id=9I8HvNfSsk4C&pg=PA96&dq=Chebyshev+distance++warehouse+logistics&ei=LJXFSLn7FIi8tAOB_8jXDA&sig=ACfU3U27UgodD209FOO7fzTysZFyPJxejw. 

External links